Ce mémoire a pour but d'établir des comparaisons entre dynamique mesurée et dynamique topologique pour le flot géodésique d'une surface de courbure constante -1. Ce travail se décompose essentiellement en quatre parties.
Dans un premier temps, nous introduisons deux façons d'appréhender des surfaces ainsi que leurs fibrés tangents unitaires, la première de nature algébrique et la seconde de nature davantage géométrique. Ce dernier, d'apparence plus géométrique nous permet de traiter les surfaces de genre au moins 2. Pour cela nous nous intéressons au demi-plan supérieur du plan complexe, appelé demi-espace de Poincaré, que nous munissons d'une métrique dite hyperbolique. Nous y définissons la notion de longueur d'une courbe et nous décrivons la nature géométrique des géodésiques. Pour cela, nous identifions le groupe d'isométries du demi-plan de Poincaré. Enfin, on étend la métrique en une métrique sur le fibré tangent unitaire et explicitons une expression des géodésiques, cette expression prend la forme d'un flot. Nous présentons aussi un autre modèle, de nature algébrique. Il s'agit du groupe de matrices $\mathrm{PSL}(2,\mathbb{R})$ pour lequel nous définissons également les flots géodésique et horocycliques comme l'action par produit matriciel de certains sous-groupes. Enfin, nous explicitons une bijection entre ces deux modèles qui conjugue respectivement les flots géodésiques et horocycliques.
Dans une seconde partie, nous définissons les principales notions de dynamique lorsqu'il existe des mesures invariantes, telles que l'ergodicité et le mélange. Nous en donnons plusieurs caractérisations et nous montrons qu'elles sont équivalentes. Par ailleurs, nous énonçons des résultats qui traitent les espaces $L^p$ comme des espaces topologiques. On munit l'espace des fonctions mesurables, par rapport à une certaine mesure, d'une topologie dont les propriétés dépendent de celles de la mesure. On démontre des résultats de densité de fonctions régulières dans certains espaces $L^p$. Enfin, on introduit succinctement la notion de fonction Riemann-intégrable.
Une fois toutes ces notions introduites, nous énonçons un théorème bien connu ainsi que sa preuve : le flot géodésique est mélangeant et, en particulier, ergodique par rapport à la mesure de Liouville. La preuve de l'ergodicité semble pouvoir s'adapter au cas de la dynamique topologique, c'est l'objectif de la section suivante.
Dans une nouvelle partie, nous commençons par établir quelques rappels fondamentaux de topologie générale. Nous introduisons ensuite les notions d'ensembles maigres, génériques et les espaces de Baire. Nous présentons la notion de propriété de Baire d'un ensemble, puis démontrons que la classe des sous-ensembles d'un espace topologique qui ont cette propriété forme une tribu. Nous définissons la notion de transitivité pour un système dynamique topologique, puis nous utilisons la notion propriété de Baire afin d'en établir une caractérisation par le biais de fonctions invariantes parmi une certaine classe de fonctions Baire-mesurables. Cette caractérisation est ensuite simplifiée en ne considérant plus que les fonctions régulières presque partout de la classe de fonctions précédente. Nous établissons des résultats de complétudes et de densités pour ces espaces de fonctions. Enfin, nous évoquons la notion de mélange faible topologique ainsi qu'une caractérisation par le biais de fonctions invariantes.
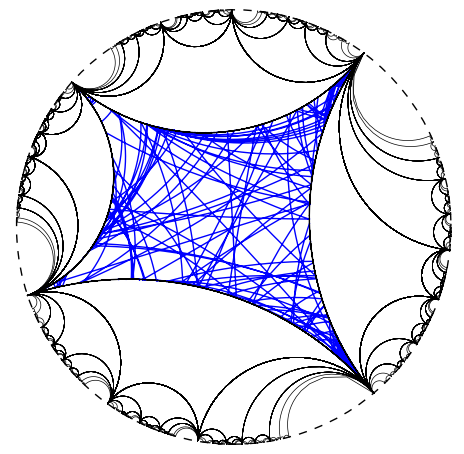
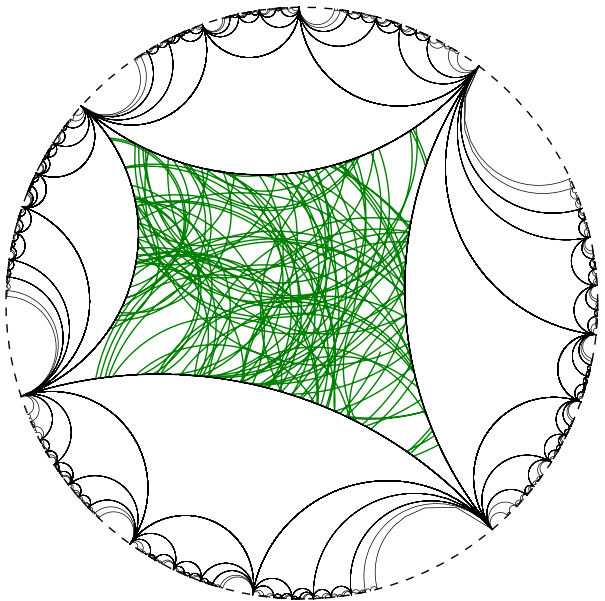
Nous appliquons alors ces caractérisations à la transitivité des flots géodésique et horocycliques et au mélange topologique faible du flot géodésique, sous certaines hypothèses.
En dernière partie, nous constatons un certain nombre de similarités dans les preuves de l'ergodicité et de la transitivité du flot géodésique pour une surface munie d'une métrique hyperbolique, en particulier lors de l'application des caractérisations par des fonctions invariantes. Dans cette partie, nous essayons de trouver un formalisme permettant de traiter les deux cas en un seul. Pour ce faire, nous généralisons les définitions de transitivité et d'ergodicité pour n'en faire qu'une, puis nous construisons une tribu et nous nous intéressons aux fonctions mesurables par rapport à celle-ci. Enfin, si la classe des fonctions régulières presque partout parmi cette classe de fonction possède suffisamment de propriétés de régularité, nous parvenons à établir que le flot géodésique satisfait à la définition généralisée d'ergodicité.
Dans ce stage, on se propose d'étudier la transformation sur le tore bidimensionnel définie dans [Coudène2013], issue d'une perturbation d'un automorphisme linéaire du tore. On montre que celle ci possède un compact invariant $K$ et que celui ci est un attracteur. Le but du stage est alors de construire une mesure de probabilité de support $K$, invariante par la transformation, qui rende la transformation mélangeante en restriction à $K$.
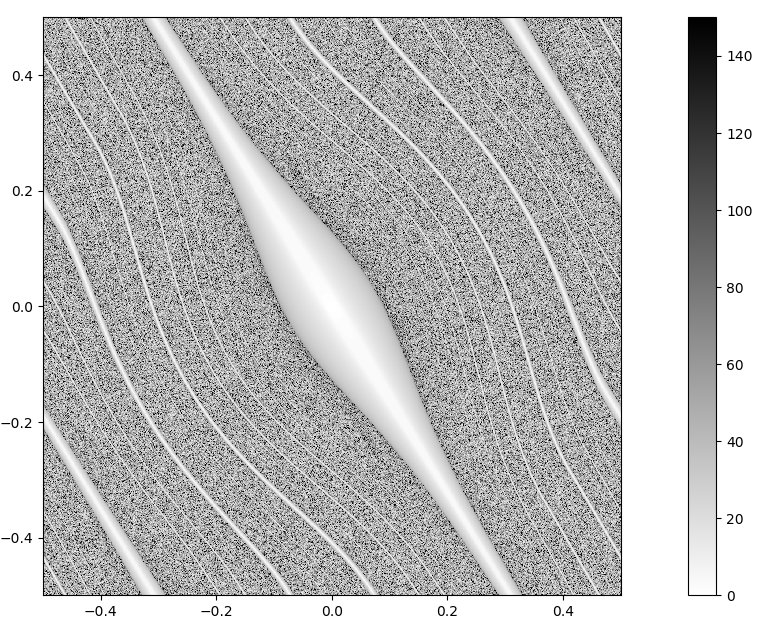
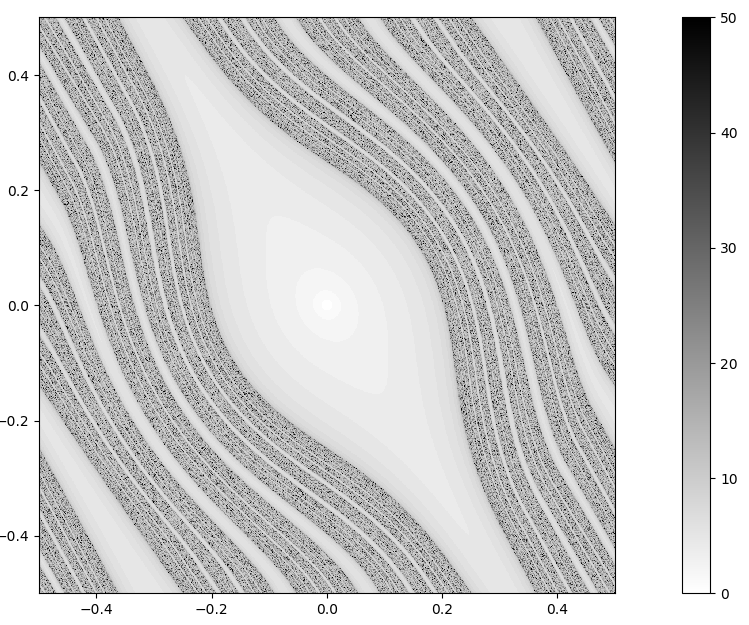
Dans la première section, on commence par donner quelques propriétés élémentaires de la transformation considérée. Celles-ci nous permettent de montrer des propriétés, énoncées dans [Coudène2013], de nature topologique sur le compact $K$, en particulier on montrera que $K$ est d'intérieur vide, connexe et possède un point d'orbite dense dans $K$. On s'intéresse également aux liens entre la transformation $f$ et son compact invariant $K$. On montre notamment que $K$ est un attracteur pour $f^{-1}$ et répulseur pour $f$. Enfin, on cherche à munir l'ensemble $K$ d'une structure dite hyperbolique. Pour cela, on construit explicitement deux fibrations de l'espace tangent du tore. On énoncera sans démonstration quelques conséquences de l'hyperbolicité de $K$. Ces propriétés de nature générale sur les ensembles hyperboliques peuvent être trouvées dans [Bowen1970markov], [BrinStuck2002], [KatokHasselblatt1997] et dans [Robinson1998dynamical]. On donnera des représentations graphiques du compact $K$ pour différents paramètres de $f$.
Dans la deuxième section, on montre que l'expression du champ de vecteurs $v^s$, donnée dans la partie précédente, est encore valide sur tout le tore et donne lieu à un champ de vecteurs globalement lipschitzien, moyennant une hypothèse supplémentaire sur l'amplitude $p_1$ de la perturbation de $f$. On considère le flot $(h_t)_t$ associé. On montre que celui-ci possède une propriété de commutation avec la transformation $f$, plus précisément on montre que $f \circ h_t = h_{\lambda^{-2} t} \circ f$. Cette relation implique un fort lien entre le flot et la transformation, que nous exploitons pour montrer l'invariance de $K$ par le flot $(h_t)_t$ et que ce flot ne possède pas d'orbite périodique. On montre également que les ensembles $\alpha$-limite et $\omega$-limite de tout point de $U$ par le flot $(h_t)_t$ sont exactement $K$. Ces propriétés donnent de nouveaux renseignements sur la structure du compact $K$.
Enfin, dans la troisième section, on étudie plus précisément les mesures invariantes par le flot $(h_t)_t$. On commence par rappeler la définition de l'invariance d'une mesure par une transformation, puis on énonce quelques propriétés générales portant sur l'ensemble des mesures invariantes pour une certaine dynamique, ces propriétés étant énoncées et démontrées dans [Walters2000introduction]. On montre alors que le flot $(h_t)_t$ possède une unique mesure invariante, supportée dans $K$ et est minimal en restriction à $K$. On montre finalement que cette mesure est invariante par $f$ et qu'elle rend cette transformation mélangeante.