Dans le cadre du diplôme de l'ENS Paris-Saclay, j'ai effectué en 2019/2020 une Année de Recherche Prédoctorale à l'Étranger (ARPE) à L'Institut de Mathématiques de l'Université de Zurich, sous la direction de Corinna Ulcigrai.
L'objectif de ce stage est d'étendre au cas des surfaces de genre au moins 2 les travaux que j'ai effectué en M1 sur le tore. En particulier j'étudie une classe de fonctions obtenues par perturbation d'un difféomorphisme pseudo-Anosov en tous ses points coniques. Chaque fonction de cette classe a la particularité de posséder un attracteur non trivial dont on se propose de donner une étude.
Dans un premier temps on s'intéresse aux fondements de la théorie de Teichmüller et plus particulièrement au théorème de classification de Nielsen-Thurston. Celui-ci permet de comprendre en quoi les difféomorphismes pseudo-Anosov ne sont pas des objets pathologiques, dont l'étude est importante pour comprendre la totalité des transformations lisses des surfaces.
On donne par la suite une construction explicite de transformations dérivées d'Anosov. On montre que pour un bon choix de paramètres, ces transformations possèdent un attracteur et que celui ci est toujours connexe et hyperbolique. L'application considérée y est transitive. L'étude de la transformation est alors reliée à celle d'un flot qu'elle renormalise. Par suspension, l'étude de ce flot se ramène alors à celle du comportement dynamique d'un échange d'intervalles généralisé. Par chance, ce dernier est semi-conjugué à un échange d'intervalles (par translations) associé à un pseudo-Anosov.
Ceci nous permet de donner un rapide aperçu de la théorie des échanges d'intervalles, notamment le processus de renormalisation de Rauzy-Veech.
Finalement, on obtient l'unique ergodicité du flot associé au problème. La relation de renormalisation nous permet d'obtenir une mesure par rapport à laquelle la transformation initiale est mélangeante.
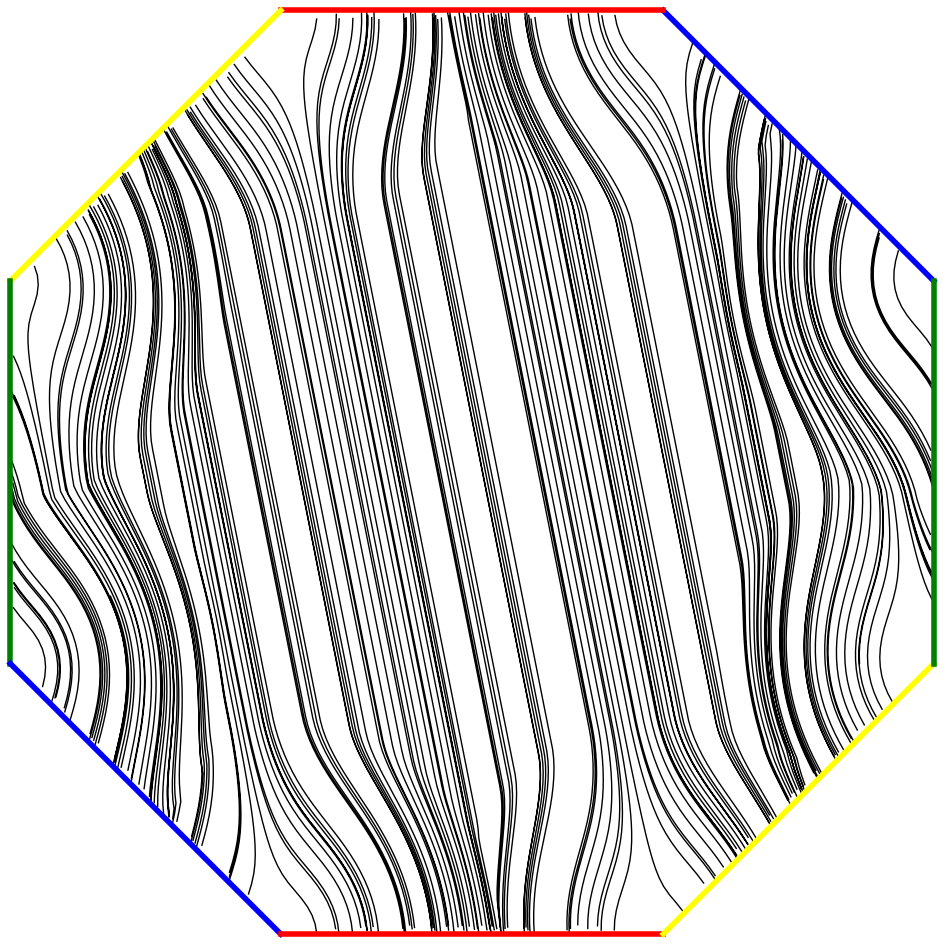
On donne une illustration dans le cas d'une surface de genre 2, dont on peut expliciter sans trop de peine un difféomorphisme pseudo-Anosov. La figure représente l'attracteur associé à une transformation dérivée d'Anosov explicite.